Tracking children's development over time
The Longitudinal Study of Australian Children Outcome Indices, Waves 2 and 3
You are in an archived section of the AIFS website
October 2011
Sebastian Misson, Ann Sanson, Donna Berthelsen, Helen Rogers, Sheldon Rothman, Mark Sipthorp, Melissa Wake, the LSAC Research Consortium
Download Research report
Summary
This paper outlines the development of the Outcome Indices for Waves 2 and 3 of Growing Up in Australia: The Longitudinal Study of Australian Children (LSAC).1
LSAC's extensive data collection provides a large range of measures on many different aspects of children's functioning, which are needed for answering important questions about child development. The LSAC Outcome Indices are designed to be simple, user-friendly summaries of key child development measures as a tool for communicating otherwise complex research findings for policy-makers, the media, the general public and other data users. The Wave 1 Outcome Indices were published with the initial release of the LSAC data in April 2005. Hence, they have been in the public domain for some time, and have received considerable use and scrutiny. With the release of Waves 2 and 3 data, longitudinal and cross-cohort comparisons of child outcomes are possible. These factors have led to the revision of the Wave 1 Outcome Indices in conjunction with the development of the Wave 2 and 3 Outcome Indices. As such, this paper is intended to describe the construction of the Outcome Indices for Waves 1, 2 and 3 data, as at the time of Wave 3 data release. Except when noted, all analyses presented in this paper use weighted data.
More detail on the construction of the original Wave 1 Outcome Indices can be found in LSAC Technical Paper No. 2 (Sanson, Misson, & the Outcome Index Working Group, 2005), available from the LSAC website. When reading this paper, it should be noted that changes to the original indices have occurred since its publication (see Appendix A for more detail on the rationale for these changes).
1 LSAC is funded as part of the Australian Government's Stronger Families and Communities Strategy by the Australian Government Department of Families, Housing, Community Services and Indigenous Affairs (FaHCSIA). The first three waves of the study were undertaken in partnership with the Australian Institute of Family Studies, with advice being provided by a consortium of leading researchers at research institutions and universities throughout Australia. The data collection for Waves 2-4 of LSAC was carried out for the Institute by the Australian Bureau of Statistics (ABS).
Background
Growing Up in Australia is one of the largest and most complex studies of its kind that has ever been undertaken in Australia. Wave 1 data collection was undertaken in 2004, with Wave 2 occurring two years later in 2006, and Wave 3 in 2008. At Wave 1, the study recruited two cohorts of approximately 5,000 children each; more than 90% of these were retained in Wave 2 and 85% in Wave 3. The first of these cohorts (the B or birth cohort) was born between March 2003 and February 2004, and were aged approximately 0-1 years at Wave 1, 2-3 years at Wave 2 and 4-5 years at Wave 3. The second cohort (the K or kindergarten-aged child cohort) was born between March 1999 and February 2000 and was aged 4-5 years at Wave 1, 6-7 years at Wave 2 and 8-9 years at Wave 3. The Outcome Indices are composite measures to indicate how children are developing. LSAC tracks the development of children across multiple domains, and the Outcome Indices provide a means of summarising this complex information. In contrast to other indices that focus on problems - such as the Vulnerability Index developed in the Canadian National Longitudinal Study of Children and Youth (NLSCY; Willms, 2002) - the LSAC Outcome Indices, wherever possible, incorporate both strengths and weaknesses, as more children have good developmental outcomes than negative outcomes. Thus, the Outcome Indices have the ability to identify groups of children with poor development as well as those doing well. In developing the LSAC Outcome Indices, the following guiding principles were followed: The indices should provide a snapshot of the children's development at the time of each main wave of data collection. The indices should contain all dimensions of developmental interest. The indices should have policy and research relevance. The indices should be made up of constructs that can be measured throughout childhood and into adulthood. The indices should be able to identify both those children doing poorly and those doing well, wherever possible. The indices should be predictive of later childhood, adolescent and adult outcomes. The indices should be parsimonious. The indices should not include distal factors (e.g., income, family structure) that are predictively related to child outcomes, but rather focus on actual developmental status.
Framework for conceptualising child outcomes
For the purpose of the LSAC Outcome Indices, an outcome is a developmental attribute of the child at a particular point in time. Hence, factors that may influence child development, and are sometimes used as indicators of child wellbeing (e.g., poverty, maternal depression, prematurity), are not included as they are not direct measures of child development. If such indicators were to form part of the indices, it would not be possible to test empirically their influence on child wellbeing. It is therefore important to make a clear separation between actual current child functioning and possible causal influences.
In developing the LSAC Outcome Indices, we consider children both as "beings" and as "becomings". When considering children as "beings", we are concerned about their wellbeing here and now, at a particular point in time, and the domains of social, emotional, physical/health and school-related functioning capture the major aspects of this wellbeing. When considering children as "becomings", we need to consider the eventual outcomes towards which we would like children to develop. It is proposed that a key outcome of interest is that children become adults capable of productive social and economic participation in society. This encompasses their future roles as learners, workers, family members and community members. While there are many other outcomes we might hope children will achieve (e.g., happiness), the broad goals of economic and social participation may best capture what it means to be a positive contributor to society.
The broad framework for the LSAC Outcome Indices can be seen in Figure 1. Three domains are proposed to be the major components of both current wellbeing and a child's future capability to be a successful civic and economic participant: health and physical development, social and emotional functioning, and learning and academic competency. Indices for each of these domains are calculated, and they are combined to form the Overall Outcome Index. Due to the difficulties of measuring and comparing the importance of each of these broad domains to the child's development, each domain is weighted equally within the Overall Outcome Index. It is acknowledged that children's development is multidimensional and interactive, and that there are "fuzzy boundaries" between these domains of functioning. At the same time, a child's development may not be uniform across domains; for example, a child may be doing well in learning, but have poorly developed physical skills. It is important to try to capture this variability.
Figure 1. Conceptual framework for the Outcome Index, showing domains and subdomains
A criterion for components in the Overall Outcome Index is that they should be measurable from Wave 1 (for at least the K cohort) to adulthood. Measures of child functioning obviously differ by age, so the specific measures of many components change over waves, but their meaning, and the meaning of the Overall Outcome Index, will be broadly consistent across the age span.
A second criterion is that the Overall Outcome Index should be predictive of later outcomes. While the variables selected are those that the literature suggests will be predictive, with only three waves of data available there is currently limited capacity to identify which variables are predictive of later outcomes. It is possible that later waves of data will suggest that some revision of the index would be worthwhile in order to increase its predictiveness.
Approach to measurement
In researching the most appropriate way to develop the Outcome Indices, two approaches to combining variables for each subdomain and domain were initially investigated.
The first was modelled on the NLSCY Vulnerability Index and involved the creation of cut-off scores for each variable to indicate problem/no-problem status. An iterative process involved identifying the number of variables within a subdomain where the child had problem status, and then (through the use of another cut-off) the number of subdomains, and finally the number of domains where the child had problem status. These last could be summed to create a negative ("problem") index. Since it was desired to also identify children who were doing particularly well, the same process could be used for creating a positive ("no-problem") index.
This approach results in a score that reflects the relative position of the child in terms of having problems or performing well. However, its major limitation is that it requires a large number of decisions about where cut-offs should be placed at each stage of the process. Some of these decisions could be made on the basis of previous literature on the prevalence of problems, but many would necessarily be arbitrary. Evidence-based cut-offs require use of measures that have been previously validated on a comparable sample or knowledge about the proportion of the child population at risk due to their poor performance on a particular measure. Such data are available for few of the available measures. Further, in most instances, there is little known about the numbers or characteristics of children performing extremely well. Hence, a score reflecting the number of variables on which a child was below (or above) the cut-offs would probably have a large error component. Further, the nature of the distribution of scores across variables leads to different proportions of the sample being below (or above) cut-offs for problem (or positive) status across variables and domains, thus resulting in the uneven weighting of variables and domains within the index. A further difficulty with this approach is how to handle missing data. Cases with fewer scores present on the file would have fewer chances to be identified as problematic, meaning that non-response would create a bias in the measure.
The second approach retains variables in their continuous form, but uses standardisation of all contributing variables to make them comparable. A subdomain score is computed as the mean of standardised scores on variables contributing to it, with the Outcome Index for each domain being the average of these standardised scores. The Overall Outcome Index score is derived from the mean of these domain indices after standardisation. A categorical form of the Overall Outcome Index is computed by applying cut-offs (e.g., top and bottom 15%) to the domain indices to identify positive and problem status, and then summing the number of domains with problem status and the number with positive status. The process is described in detail in the "Calculation of the Outcome Indices" section below. It should be noted that the cut-off of 15% at the lower end does not necessarily reflect a problem for the child in terms of development or achievement. Similarly at the top end, caution is needed in using the cut-offs, as some measures (such as the Strengths and Difficulties Questionnaire [SDQ]) are not designed to discriminate between children doing substantially better than others.
The first major advantage of this continuous approach is that there is no reliance on cut-offs until the last stage of computation, and hence information is not lost through reducing continuous scores on variables to dichotomous categories, and the use of arbitrary cut-offs does not lead to erroneous conclusions about a child’s status. Secondly, each subdomain within a domain, and each domain within the Overall Outcome Index, can be approximately evenly weighted so that each contributes equally, and explanation of how the indices are calculated is relatively straightforward. Given these advantages, this approach was adopted.
The overlap in ages between the B cohort at Wave 3 and the K cohort at Wave 1 creates another issue about how to best standardise the Outcome Indices. Three options were considered for standardising the Outcome Indices and its component measures when the cohorts overlap in age:
- Standardise for each cohort and wave separately, as per ages, without an overlap.
- Combine the K cohort Wave 1 and B cohort Wave 3 data and standardise these as a whole group.
- Use the K cohort to create norms for the B cohort.
The first of these options would mean that each Outcome Indices score has a known mean and standard deviation for every cohort and every wave. This would mean that comparisons could not be made on a whole-cohort basis (e.g., it would be impossible to use the Outcome Indices to test whether the B cohort was doing better or worse than the K cohort when they were at the same age). Also, the situation could arise that two children who have identical scores on the component items receive different Outcome Indices scores because they are from different cohorts.
For the other options, it is possible to make cross-cohort comparisons; however, cross-wave comparisons would need to be carefully interpreted. This is because there would be some ages where the mean and standard deviation for each cohort would be arbitrary and others where it would be meaningful. For example, if the B cohort averaged 102 on the Outcome Index at Wave 3, a child whose scores were 100 at Wave 1, 102 at Wave 2 and 102 at Wave 3, might be misinterpreted as having improved between Waves 2 and 3, whereas in actuality it is only the frame of reference that has changed.
In the second option, the mean and standard deviation for the combined cohort sample would be arbitrary at every age, but the means for each cohort would have meaning with respect to each other (i.e., it would be possible to tell if the B cohort is doing better or worse than the K cohort). However, this option would require the re-calculation of the Wave 1 Outcome Indices for the K cohort, and the re-calculation of every subsequent wave four years after initial publication.
The third option results in only the mean and standard deviation for the B cohort having meaning (although not for Waves 1 and 2); however, it would not require recalculation of the K cohort scores from Wave 1.
After consultation with the LSAC Data Expert Reference Group and Consortium Advisory Group, it was decided to calculate two different versions of the Outcome Indices:
- the within-cohort Outcome Indices will be standardised by cohort so that a score of 100 will have consistent meaning across waves; and
- the between-cohort Outcome Indices will be standardised with the two cohorts combined, so scores will have greater comparability across cohorts.
Calculation of Outcome Indices
The following process is used to calculate the Outcome Indices:
- Classify all outcome measures into the structure outlined in Figure 1.
- Choose the measures that provide the best measurement of the subdomain.
- Create a z-score for each chosen outcome measure such that good outcomes are represented by positive scores, and poor outcomes by negative scores.
- Compute a score for each subdomain by taking the mean of these standardised scores within each subdomain and standardise this to a z-score adjusting for missing data when necessary (see Appendix B for more details on handling missing data).
- Compute an index for each domain by obtaining the mean of the standardised scores within each domain and standardise to have a mean of 100 and a standard deviation of 10, again adjusting for missing data when necessary.
- Create cut-off variables that identify the 15% of children with lowest performance and the 15% of children performing most highly in each domain (roughly representing the number of children who have scores below and above the sample mean by one standard deviation).
- For cases with a score in all three domains: create a Negative Outcome Index indicating the number of domains in which a child performs poorly and a Positive Outcome Index indicating the number of domains in which a child performs well.
- For cases with a score in all three domains: create an Overall Outcome Index by obtaining the mean of all three domain scores and standardising to have a mean of 100 and a standard deviation of 10.
- Create cut-off variables representing that highest and lowest scoring 15% of children on the Overall Outcome Index score.
Out of this process, a suite of variables are made available to users: three domain indices, three positive cut-off domain indices, three negative cut-off domain indices, a Positive Outcome Index, a Negative Outcome Index, an Overall Outcome Index, plus an Overall Outcome Index positive cut-off and an Overall Outcome Index negative cut-off. Providing a suite of variables allows users to tailor their analyses for their particular purpose and what they consider the needs of their audience.
Selection of component variables
For ease of interpretability, it was desirable to include a small set of valid and reliable variables in the Outcome Indices. Given the scope of the LSAC dataset, there were a considerable number of variables to consider for inclusion. The following criteria were used in choosing among these:
- Variables with high response rates (derived from the Parent 1 interview or during-interview questionnaire) were preferred over those with lower response rates (Parent 1 leave-behind questionnaire, teacher or carer data). If it was possible to get good coverage of a domain with high-response variables, only these were used. However, for some content areas, only lower response variables were available, and on others it was considered desirable to include two informants (e.g., parent and teacher). Procedures to manage missing data, when necessary, are described in Appendix B.
- Distribution of scores on the variable allowed discrimination between children with poor and average functioning, and preferably also between those with average and good functioning. In general terms, it was assumed that at least 20% of the sample should be identified as doing poorly on any one variable, and a similar proportion as doing well. Some selected variables gave good discrimination between poor and average scores but less adequate discrimination between average and good scores.
- Adequate internal consistency of scales, where relevant.
The final set of variables selected for inclusion in the Outcome Index is shown in Table 1. Full descriptions of these variables are in the LSAC Data Dictionary2 and brief summaries are provided in the following pages.
| Domain | Subdomain | Aged 0-1 | Aged 2-3 | Aged 4-5 | Aged 6-7 and 8-9 |
|---|---|---|---|---|---|
| Health/Physical | Health | Overall rating of health Special health care needs Health problem | Overall rating of health Special health care needs Health problems Weight status | Overall rating of health Special health care needs Health problems Weight status | Overall rating of health Special health care needs Health problems Weight status |
| Motor | Overall rating of health Special health care needs Health problems | PedsQL Physical Health | Pedsql Physical Health | Gross motor coordination PedsQL Physical Health | |
| Social/Emotional | Internalising | STSI Approach STSI Irritability STSI Cooperativeness | Factor-analysed BITSEA Internalising | SDQ Emotional Symptoms | SDQ Emotional Symptoms |
| Externalising | STSI Approach STSI Irritability STSI Cooperativeness | Factor-analysed BITSEA Externalising | SDQ Conduct Problems SDQ Hyperactivity | SDQ Conduct Problems SDQ Hyperactivity | |
| Social Competence | STSI Approach STSI Irritability STSI Cooperativeness | Factor-analysed BITSEA Social Competence | SDQ Peer Problems SDQ Prosocial | SDQ Peer Problems SDQ Prosocial | |
| Learning/Academic | Language and Literacy | CSBS Total Standardised Score | Child's communication skills MCDI-III Vocabulary MCDI-III Grammatical Markers | WAI PPVT | PPVT ARS Language and Literacy |
| Numeracy and Cognition | CSBS Total Standardised Score | Child's communication skills MCDI-III Vocabulary MCDI-III Grammatical Markers | Teacher rating of numeracy skills | WISC-IV Matrix Reasoning ARS Mathematical Thinking |
Notes: PedsQL = Pediatric Quality of Life inventory; STSI = Short Temperament Scale for Infants; BITSEA = Brief Infant Toddler Social Emotional Adjustment scale; SDQ = Strengths and Difficulties Questionnaire; CSBS = Communication and Symbolic Behaviour Scale; MCDI-III = MacArthur Communicative Development Inventory, Level III; WAI = Who Am I? test; PPVT = Peabody Picture Vocabulary Test; ARS = Academic Rating Scale; WISC-IV = Wechsler Intelligence Scale for Children IV.
Unfortunately, not all of the subdomains are easily measurable from an early age. Hence, in Wave 1 for the B cohort, there is no measure of motor skills for the Health/Physical domain, the only measures for the Social/Emotional domain are temperament assessments, and only a general measure of pre-language skills is available for the Learning/Academic domain. Therefore, no subdomain scores are calculated for the B cohort at Wave 1, with the mean of the standardised scores of the original measures creating the domain scores directly. Hence the meaning of the index varies to some extent across cohorts, at least in Wave 1. This needs to be taken into consideration when making use of the Outcome Index for the B cohort, particularly in conjunction with indices from later waves.
Health/Physical domain
Table 2 shows the response rates and, where appropriate, reliabilities of the measures in the Health/Physical domain. At age 0-1, three measures contributed to the Health/Physical domain score. The Overall Rating of Health is a single parent-rated item that rates a child's health from 1 = Excellent to 5 = Very poor. The Special Health Care Needs screener is a single derived yes or no item based on six component items indicating whether the child needed medication or more health care than the average child due to a condition that had lasted or was expected to last twelve months or more. The Health Problems index is a derived item based on the number of health problems that the child was reported to be experiencing around the time of the main interview (see Appendix A for more information).3 All three measures came from the Parent 1 face-to-face interview and so have good response rates; however, they have a small range of scores, particularly in regard to discriminating between children with good physical outcomes and average outcomes. Therefore, a positive cut-off variable was not possible for this domain for children at this age.
| Subdomain | N | Response rate* (%) | Cronbach alpha | |
|---|---|---|---|---|
| Aged 0-1 (B cohort) | ||||
| Overall rating of health | NA | 5,105 | 100.0 | NA |
| Special health care needs | NA | 5,027 | 98.4 | NA |
| Health problems | NA | 5,080 | 99.5 | NA |
| Aged 2-3 (B cohort) | ||||
| Overall rating of health | Health | 4,606 | 100.0 | NA |
| Special health care needs | Health | 4,375 | 95.0 | NA |
| Health problems | Health | 4,578 | 99.4 | NA |
| Weight status | Health | 4,521 | 98.2 | NA |
| PedsQL Physical Health | Motor | 3,362 | 73.0 | .72 |
| Aged 4-5 (B cohort) | ||||
| Overall rating of health | Health | 4,982 | 100.0 | NA |
| Special health care needs | Health | 4,927 | 98.9 | NA |
| Health problems | Health | 4,966 | 99.7 | NA |
| Weight status | Health | 4,930 | 98.9 | NA |
| PedsQL Physical Health | Motor | 4,179 | 83.9 | .73 |
| Aged 4-5 (K cohort) | ||||
| Overall rating of health | Health | 4,385 | 100.0 | NA |
| Special health care needs | Health | 4,384 | 100.0 | NA |
| Health problems | Health | 4,375 | 99.7 | NA |
| Weight status | Health | 4,324 | 98.6 | NA |
| PedsQL Physical Health | Motor | 3,820 | 87.1 | .72 |
| Aged 6-7 (K cohort) | ||||
| Overall rating of health | Health | 4,464 | 100.0 | NA |
| Special health care needs | Health | 4,307 | 96.5 | NA |
| Health problems | Health | 4,455 | 99.8 | NA |
| Weight status | Health | 4,417 | 98.9 | NA |
| PedsQL Physical Health | Motor | 3,332 | 74.6 | .82 |
| Gross motor coordination | Motor | 4,462 | 100.0 | .68 |
| Aged 8-9 (K cohort) | ||||
| Overall rating of health | Health | 4,331 | 100.0 | NA |
| Special health care needs | Health | 4,331 | 100.0 | NA |
| Health problems | Health | 4,327 | 99.9 | NA |
| Weight status | Health | 4,289 | 99.0 | NA |
| PedsQL Physical Health | Motor | 4,322 | 99.8 | .73 |
| Gross motor coordination | Motor | 3,800 | 87.7 | .82 |
Notes: *Response rate among respondents for the wave. NA = Not applicable. PedsQL = Pediatric Quality of Life inventory.
The same measures were used for the Health/Physical domain for children aged 2-3 and 4-5 years. The three measures from the Health/Physical domain for 0-1 year olds were all used again for these children and classified in the Health subdomain. Also added to this subdomain was a Weight Status variable based on the physical measurements of the child taken at the time of the interview. Children's Weight Status was classified on the basis of these measurements using the cut-offs described by Cole, Bellizzi, Flegal, and Dietz (2000) for overweight and Cole, Flegal, Nicholls, and Jackson (2007) for underweight. Children were scored as receiving one point if they were Underweight I, 2 points for Underweight II, 3 points for Underweight III, 1.5 points for Overweight, 3 points for Obese, and 0 points for being between the over and underweight cut-offs. This method of scoring ensures that variations from an average ideal weight that are not considered clinically important do not create differences in Outcome Index scores, and it identifies appropriate proportions of children with over- and underweight problems. This score was then standardised and reversed in line with the other outcome measures.
For 2-3 and 4-5 year olds, the Motor subdomain is measured using the Pediatric Quality of Life (PedsQL) inventory Physical Health subscale, an 8-item parent-report measure largely assessing motor coordination, but also containing two items about more general health. This measure showed an adequate reliability (above .7); however, it was only available in the Parent 1 leave-behind questionnaire and so had a lower response rate than other measures contained in the Parent 1 interview.
The Health/Physical domain measures used for the 6-7 and 8-9 year olds were identical to those for the 2-3 and 4-5 year olds, with the addition of the Gross Motor Coordination scale to the Motor subdomain. This is a three item parent-rated scale asking how well the child can run, jump and balance on one leg compared to their peers, from 1 = Better than other children to 3 = Not as well as other children. This measure is collected in the Parent 1 interview and so allows the calculation of a Motor subdomain score for those cases that are missing PedsQL data due to a Parent 1 leave-behind questionnaire not being returned.
Social/Emotional domain
Table 3 includes the response rates and reliabilities of the measures in the Social/Emotional domain. For the Social/Emotional domain for the 0-1 year olds, items from three subscales of the Short Temperament Scale for Infants (STSI) were used: Approach (shyness/sociability), Irritability and Cooperativeness. While these are not strictly items on behaviour, they tap aspects of social and emotional functioning. Each STSI subscale consists of four items, with each item rated on a 6-point frequency scale. These items were in the Parent 1 self-complete questionnaire and so were not available for 17% of cases.
| Subdomain | N | Response rate* (%) | Cronbach alpha | |
|---|---|---|---|---|
| Aged 0-1 (B cohort) | ||||
| STSI Approach | NA | 4,259 | 83.4 | .72 |
| STSI Irritability | NA | 4,254 | 83.3 | .57 |
| STSI Cooperativeness | NA | 4,255 | 83.3 | .64 |
| Aged 2-3 (B cohort) | ||||
| Factor-analysed BITSEA Internalising | Internalising | 4,482 | 97.3 | .63 |
| Factor-analysed BITSEA Externalising | Externalising | 4,482 | 97.3 | .66 |
| Factor-analysed BITSEA Social Competence | Social Competence | 4,482 | 97.3 | .65 |
| Aged 4-5 (B cohort) | ||||
| SDQ Emotional Symptoms | Internalising | 3,824 | 87.2 | .57 |
| SDQ Hyperactivity | Externalising | 3,823 | 87.2 | .72 |
| SDQ Conduct Problems | Externalising | 3,825 | 87.2 | .66 |
| SDQ Prosocial | Social Competence | 3,828 | 87.3 | .68 |
| SDQ Peer Problems | Social Competence | 3,824 | 87.2 | .52 |
| Aged 4-5 (K cohort) | ||||
| SDQ Emotional Symptoms | Internalising | 4,965 | 99.6 | .59 |
| SDQ Hyperactivity | Externalising | 4,966 | 99.7 | .73 |
| SDQ Conduct Problems | Externalising | 4,966 | 99.7 | .69 |
| SDQ Prosocial | Social Competence | 4,966 | 99.7 | .67 |
| SDQ Peer Problems | Social Competence | 4,966 | 99.7 | .50 |
| Aged 6-7 (K cohort) | ||||
| SDQ Emotional Symptoms | Internalising | 4,308 | 96.5 | .63 |
| SDQ Hyperactivity | Externalising | 4,308 | 96.5 | .76 |
| SDQ Conduct Problems | Externalising | 4,309 | 96.5 | .60 |
| SDQ Prosocial | Social Competence | 4,310 | 96.6 | .69 |
| SDQ Peer Problems | Social Competence | 4,310 | 96.6 | .56 |
| Aged 6-7 (K cohort) | ||||
| SDQ Emotional Symptoms | Internalising | 3,802 | 87.8 | .67 |
| SDQ Hyperactivity | Externalising | 3,799 | 87.7 | .78 |
| SDQ Conduct Problems | Externalising | 3,802 | 87.8 | .64 |
| SDQ Prosocial | Social Competence | 3,801 | 87.8 | .72 |
| SDQ Peer Problems | Social Competence | 3,801 | 87.8 | .60 |
Note: *Response rate among respondents for the wave. STSI = Short Temperament Scale for Infants; BITSEA = Brief Infant Toddler Social Emotional Adjustment scale; SDQ = Strengths and Difficulties Questionnaire.
For the 2-3 year olds, the Brief Infant Toddler Social Emotional Adjustment (BITSEA) scale was used. It contains 34 parent-report items assessing the presence of emotional problems, with items score from 1 = Not true/rarely to 3 = Very true/often. The BITSEA scale was originally scored into two subscales - Problems and Competencies - but it can also be factor-analysed into three scales - Internalising, Externalising and Social Competence - which all demonstrate acceptable reliability. More information on this is in Appendix C.
The social and emotional functioning of the 4-5, 6-7 and 8-9 year olds were measured by the Strengths and Difficulties Questionnaire (SDQ) responded to by Parent 1. The SDQ consists of 5 subscales, each with 5 items that are rated on a 3-point scale. For the 4-5 year olds, the SDQ was contained in the interview instrument, while for the 6-7 and 8-9 year olds it was in the Parent 1 during-interview questionnaire, so the response rate was slightly lower. For the purposes of the Outcome Index, the Emotional Symptoms subscale was classified to the Internalising subdomain, the Hyperactivity and Conduct Problems subscales were classified to the Externalising subdomain, while the Prosocial and Peer Problems subscales were classified to the Social Competence subdomain.
Learning/Academic domain
Table 4 shows the response rates and reliabilities of the measures in the Learning/Academic domain. For the 0-1 year olds only, the Communication and Symbolic Behaviour Scale (CSBS) was used as a measure. This provides a normed, standardised score based on 24 parent-report items on the child's exhibition of various behaviours demonstrating emerging communication skills. This instrument has a very strong theoretical framework (McCathren, Warren, & Yoder, 1996) and is particularly useful for a longitudinal study since the focus is on predictive rather than concurrent validity. However, although this instrument was included in the main interview, not all parents completed it because it is inappropriate for children under 6 months of age.
| Subdomain | N | Response rate* (%) | Cronbach alpha | |
|---|---|---|---|---|
| Aged 0-1 (B cohort) | ||||
| CSBS Total Standardised Score | NA | 4,507 | 88.2 | .89 |
| Aged 2-3 (B cohort) | ||||
| Child's communication skills | NA | 3,363 | 73.0 | .74 |
| MCDI-III Vocabulary | NA | 3,301 | 71.7 | .98 |
| MCDI-III Grammatical Markers | NA | 3,245 | 70.4 | .89 |
| Aged 4-5 (B cohort) | ||||
| WAI | Language and Literacy | 4,197 | 95.7 | NA |
| PPVT | Language and Literacy | 4,266 | 97.3 | NA |
| Teacher rating of numeracy | Numeracy and Cognition | 3,359 | 76.6 | .61 |
| Aged 4-5 (K cohort) | ||||
| WAI | Language and Literacy | 4,880 | 97.9 | NA |
| PPVT | Language and Literacy | 4,390 | 88.1 | NA |
| Teacher rating of numeracy | Numeracy and Cognition | 3,159 | 63.4 | .65 |
| Aged 6-7 (K cohort) | ||||
| PPVT | Language and Literacy | 4,403 | 98.6 | NA |
| ARS Language and Literacy | Language and Literacy | 3,571 | 80.0 | .96 |
| WISC-IV Matrix Reasoning | Numeracy and Cognition | 4,393 | 98.4 | NA |
| ARS Mathematical Thinking | Numeracy and Cognition | 3,555 | 79.6 | .95 |
| Aged 8-9 (K cohort) | ||||
| PPVT | Language and Literacy | 4,270 | 98.6 | NA |
| ARS Language and Literacy | Language and Literacy | 4,273 | 81.6 | NA |
| WISC-IV Matrix Reasoning | Numeracy and Cognition | 3,532 | 98.7 | .96 |
| ARS Mathematical Thinking | Numeracy and Cognition | 3,505 | 80.9 | .97 |
Notes: CSBS = Communication and Symbolic Behaviour Scale; MCDI-III = MacArthur Communicative Development Inventory, Level III; WAI = Who Am I? test; PPVT = Peabody Picture Vocabulary Test; ARS = Academic Rating Scale; WISC-IV = Wechsler Intelligence Scale for Children IV. NA = Not applicable.
For 2-3 year olds, three scales on Language and Literacy were available, but all were in the Parent 1 leave-behind questionnaire and therefore had lower response rates. The Child's Communication Skills scale consists of 6 parent-rated items assessing the child's ability to give and receive verbal information, rated from 1 = Never to 3 = Always. The MacArthur Communicative Development Inventory, Level III (MCDI-III) Vocabulary scale consists of a list of 98 words. A child receives one point for every word that the parent reports having heard the child use. The MCDI-III Grammatical Markers scale consists of 12 items with pairs of phrases or sentences with better and worse grammar. A child receives one point for each item where the parent reports the child uses the example with better grammar.
For the 4-5-year olds, Language and Literacy skills were assessed by two direct assessment tests. An abbreviated form of the Peabody Picture Vocabulary Test (PPVT) was administered by the interviewer to obtain a Rasch-modelled score. This instrument tests receptive language by requiring a child to point to one picture out of four choices that best corresponds to a given word. The Who Am I? (WAI) test was also administered by the interviewer and the score derived following Rasch modelling. The WAI is a measure of school readiness that measures a child's ability to perform a range of tasks - such as copying and symbol recognition - that assess the cognitive processes underlying early literacy and numeracy. Numeracy was measured by a Teacher Rating of Numeracy Skills, consisting of five yes/no items assessing the child's ability to perform numeric tasks such as counting, classifying and simple addition, along with the ability to recognise numbers. This scale had a lower response rate as it was in the teacher questionnaire.
For 6-7 and 8-9 year olds Language and Literacy skills were again assessed by the PPVT, as well as the Academic Rating Scale (ARS) Language and Literacy subscale. This consists of 10 teacher-rated items assessing whether the child can perform various language tasks, focusing mainly on reading and writing, but also on oral communication. A direct assessment and a teacher-rated measure were available for the Numeracy and Cognition subdomain. The direct assessment was the Matrix Reasoning test, a subtest of the Wechsler Intelligence Scale for Children IV (WISC-IV). It produces an age-normed score from a test of 4 types of items (pattern completion, classification, analogical reasoning and serial reasoning) to provide a measure of visual information processing and abstract reasoning. The teacher assessment was the ARS Mathematical Thinking subscale, which consists of 8 teacher-rated items assessing the study child's ability to perform various mathematical tasks, scored from 1 = Not yet to 5 = Proficient. Again, the low response rate for the ARS measures is because the scales were contained in the teacher questionnaire. However, the teacher's perspective on the child's learning was considered important when available. For both the ARS subscales, a Rasch-modelled score was used for the 8-9 year olds. Rasch-modelled scores were not available at the time of the release of Wave 2 data, so these scales use a mean of the items for the 6-7 year olds.
Correlations among scores
Table 5 shows the intra-wave and cross-cohort correlations of the Outcome Indices. Correlations between the three domains were modest for the children at ages 0-1 (.07 to .12), but were higher for subsequent ages (.12 to .41). At all ages, the Social/Emotional domain index correlated most strongly with the other domains, meaning it was most highly correlated with the Overall Outcome Index.
| Health/Physical | Social/Emotional | Learning/Academic | Overall | |
|---|---|---|---|---|
| Aged 0-1 (B cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.12 | 1.00 | ||
| Learning/Academic | 0.07 | 0.12 | 1.00 | |
| Overall | 0.61 | 0.66 | 0.62 | 1.00 |
| Aged 2-3 (B cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.31 | 1.00 | ||
| Learning/Academic | 0.19 | 0.38 | 1.00 | |
| Overall | 0.70 | 0.78 | 0.72 | 1.00 |
| Aged 4-5 (B cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.40 | 1.00 | ||
| Learning/Academic | 0.13 | 0.25 | 1.00 | |
| Overall | 0.71 | 0.78 | 0.63 | 1.00 |
| Aged 4-5 (cross-cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.37 | 1.00 | ||
| Learning/Academic | 0.13 | 0.27 | 1.00 | |
| Overall | 0.70 | 0.77 | 0.65 | 1.00 |
| Aged 4-5 (K cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.35 | 1.00 | ||
| Learning/Academic | 0.12 | 0.28 | 1.00 | |
| Overall | 0.69 | 0.77 | 0.66 | 1.00 |
| Aged 6-7 (K cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.32 | 1.00 | ||
| Learning/Academic | 0.14 | 0.23 | 1.00 | |
| Overall | 0.70 | 0.74 | 0.66 | 1.00 |
| Aged 8-9 (K cohort) | ||||
| Health/Physical | 1.00 | |||
| Social/Emotional | 0.41 | 1.00 | ||
| Learning/Academic | 0.21 | 0.26 | 1.00 | |
| Overall | 0.74 | 0.77 | 0.67 | 1.00 |
As can be seen from Table 6, inter-wave correlations between like measures were relatively small for the B cohort for the Wave 1 index. The early years of life are a period of substantial change and instability, so high correlations between domains and over time are not to be expected. Limited availability of strong measures at these ages, and changes in measurement over time are other obvious sources of variability. Correlations were higher for the B cohort between Waves 2 and 3, suggesting this instability is lessening. For the K cohort, correlations were slightly lower between Waves 1 and 2 than Waves 2 and 3, but even the correlations between Waves 1 and 3 - measured four years apart - were quite strong.
| Wave 1-Wave 2 | Wave 1-Wave 3 | Wave 2-Wave 3 | |
|---|---|---|---|
| B cohort | |||
| Health/Physical | .28 | .25 | .47 |
| Social/Emotional | .26 | .21 | .53 |
| Learning/Academic | .27 | .07 | .39 |
| Overall | .36 | .26 | .60 |
| K cohort | |||
| Health/Physical | .54 | .50 | .69 |
| Social/Emotional | .62 | .55 | .71 |
| Learning/Academic | .57 | .56 | .69 |
| Overall | .69 | .64 | .78 |
2 See the Data Dictionary at <www.aifs.gov.au/growingup/data/datadict/>.
3 This measure was not part of the Outcome Index as published at the time of Wave 1 data release.
Illustrative examples of the use of the index
This section presents examples that illustrate the use of the various forms of the indices for the two LSAC cohorts and at the two waves of data collection. It is possible to compare children in particular subgroups (e.g., by sociodemographic or geographic variables) in terms of whether they are over- or under-represented in the positive or negative outcome categories by using the categorical form of the Outcome Indices (top and bottom 15% of the distribution). Using the continuous form, average outcome scores across groups can be compared. A sample of simple analyses is presented to illustrate the diversity of ways in which the index can be used. Because they are simple univariate or bivariate comparisons, caution needs to be used in interpreting these findings. The analyses are given purely to be illustrative.
Illustration of cut-off domain indices: Are there gender differences in learning outcome for 4-5 year olds?
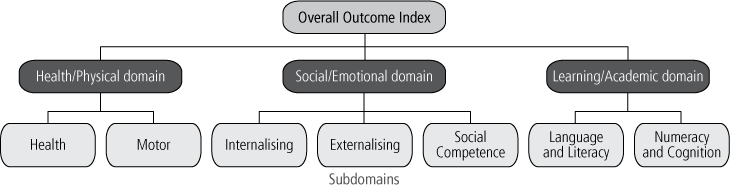
The cut-off domain indices allow analysts to identify the top and bottom 15% of the LSAC sample in terms of functioning on each domain. Figure 2 illustrates the use of the categorical form of a domain index, and shows that substantially fewer boys (10%) than girls (20%) were in the top 15% of the distribution on the Learning/Academic domain (positive index) and substantially more boys (20%) than girls (10%) were in the bottom 15% (negative index).
Figure 2. Percentages identified by the positive and negative Learning/Academic domain cut-offs, by gender, 4-5 year-olds
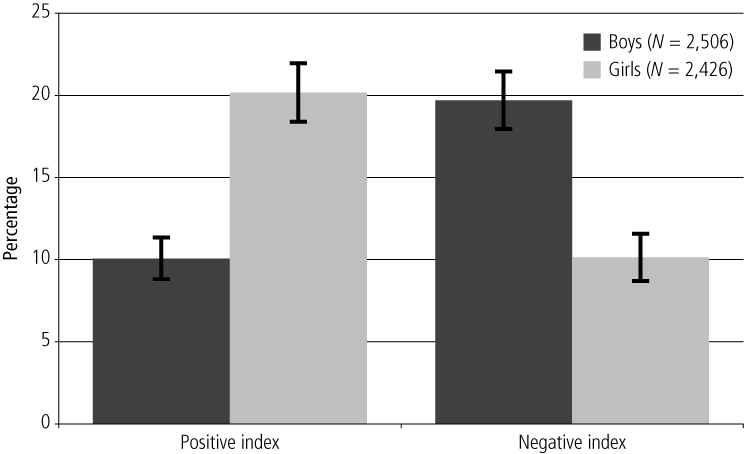
Illustration of across-domain comparisons: Are 6-7 year olds with poor physical outcomes likely to have poorer learning and social/emotional outcomes?
This analysis shows how the scores from multiple domains can be combined in a single analysis, using one categorical domain index (Health/Physical) and two continuous domain indices (for Learning/Academic and Social/Emotional). Figure 3 shows that 6-7 year olds with poor Health/Physical outcomes had lower scores on both the Learning/Academic and Social/Emotional domains than those who did not have a poor Health/Physical outcome.
Figure 3. Mean scores for the Learning/Academic and Social/Emotional indices, by negative or positive Health/Physical index cut-off, 6-7 year olds
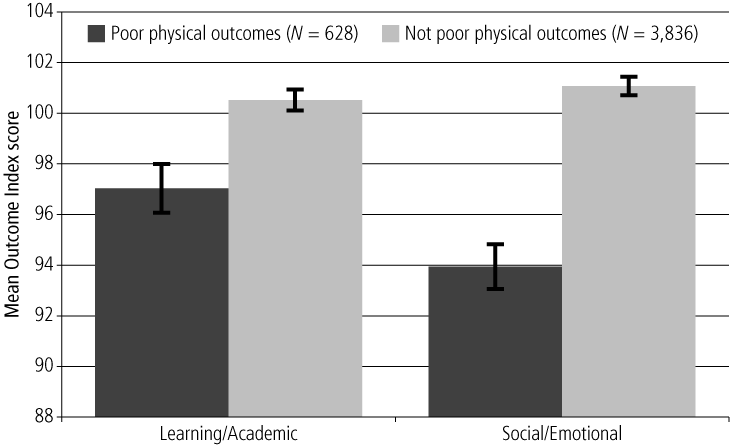
Illustration of longitudinal comparisons: Do K cohort children whose parents separated between Waves 1 and 2 have poorer scores at the next wave?
This example demonstrates the use of Outcome Indices from different waves of data collection by examining the change indices for K cohort children whose parents had separated since Wave 1 versus those whose parents stayed together. Figure 4 shows that those children whose parents separated since Wave 1 had a significant deterioration in their Social/Emotional Index scores, but were unaffected in the other domains.
Figure 4. Change between waves in mean domain indices for K cohort children who lived with both biological parents at Wave 1, by whether parents had separated by Wave 2
Illustration of positive and negative indices (categorical form): Do 2-3 year olds from single- and dual-parent families differ in outcomes?
The categorical Outcome Indices combine the information from the positive or negative cut-off scores for the three domains into a single variable. Figure 5 demonstrates how these scores can be used to show the percentage of children living in single- and dual-parent families who are in the lowest 15% on 0, 1, 2 or 3 domains (negative index) and in the top 15% on 0, 1, 2 or 3 domains (positive index). It indicates that there is a trend for 2-3 year olds from dual-parent families to have fewer poor outcomes and more strengths than those in single-parent families.
Figure 5. Percentage of children with positive or negative indices, by single- and dual-parent families, 2-3 year olds
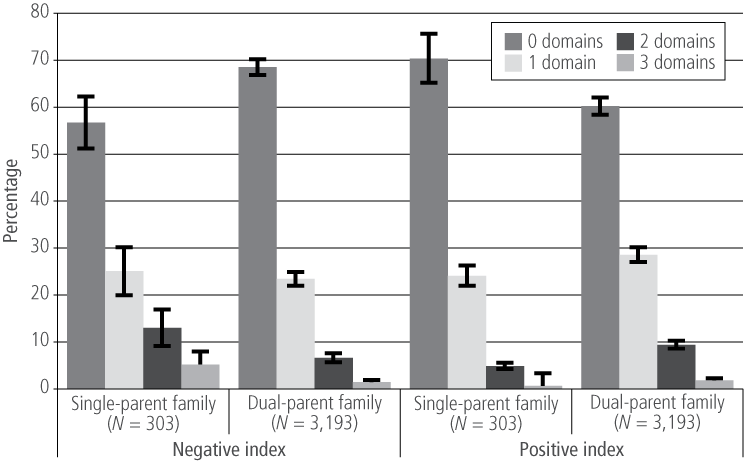
Illustration of continuous form of the Overall Outcome Index: Do 4-5 year old child outcomes differ by household income?
The continuous Overall Outcome Index combines the three continuous domain scores into a single continuous measure with a mean of 100 and standard deviation (SD) of 10. Figure 6 shows how this score can be used to compare child outcomes using parental income to compare groups of children. It reveals that among 4-5 year olds, there is a modest linear gradient of outcomes by income, from an average score of under 97 for the lowest income group to over 103 for the highest group.
Figure 6. Mean Overall Outcome Index scores, by weekly parental income, 4-5 year olds

Illustration of continuous domain score: Is parenting self-efficacy related to 0-1 year olds' social and emotional development?
Continuous domain indices represent a child's functioning on a domain in a single continuous score, again with a mean of 100 and SD of 10. Figure 7 provides an example of its use by comparing children's outcomes in the Social/Emotional domain based on their primary parents' rating of their own ability as a parent on a 5-point scale. About two-thirds of parents rated themselves as very good or better than average parents, and their children were on average above 100 on the continuous Social/Emotional Index. Infants of parents who saw themselves as average parents had an average score of about 98. The small groups of parents who saw themselves as having some trouble or not very good at being a parent had infants with markedly lower scores.
Figure 7. Mean Social/Emotional Outcome Index scores, by Parent 1's rating of their own parenting ability, 0-1 year olds
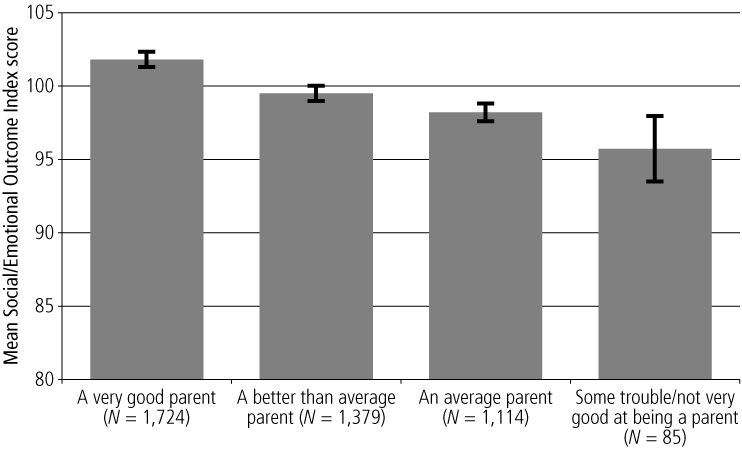
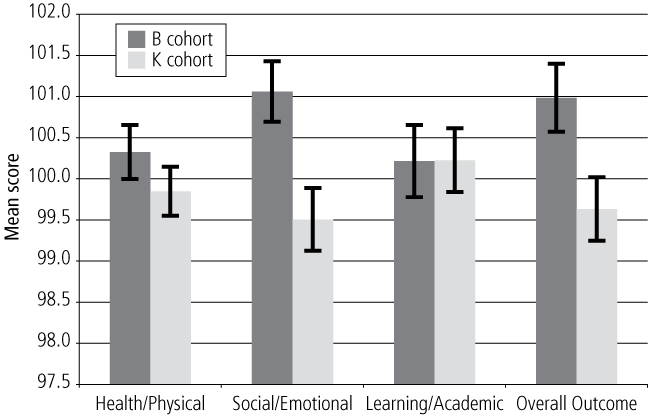
Illustration of cross-cohort comparisons: Continuous Outcome Indices
Figure 8 shows comparisons of the two cohorts on the cross-cohort Outcome Indices at ages 4-5. The data are presented to show the differences in scores between the cohorts without controlling for any confounding differences between the cohorts. Interpretations about the relative strengths and weaknesses between the two cohorts should be made with caution.4 The figure shows that the B cohort obtained significantly higher scores for the Health/Physical, Social/Emotional and Overall Outcome Indices.
Figure 8. Cohort comparison on cross-cohort Outcome Indices, 4-5 year olds
Conclusions
The analyses presented here provide indications of the performance of the Outcome Indices. The intra- and inter-wave correlations suggest acceptable relationships between the indices obtained at both waves (although stronger for the K cohort than the B cohort), providing an indication that there is a pool of common variance in child development across broad domains of functioning and across different times that is being measured by the LSAC Outcome Indices.
While it was initially intended to model the Outcome Indices on the categorical approach adopted for the Canadian Vulnerability Index, further investigation on the implementation of this approach identified significant difficulties with it. Its inherent weaknesses included reliance on multiple arbitrary cut-offs and the impossibility of weighting different elements equally. The current index uses a continuous approach, which is more statistically and mathematically principled.
It was decided to include multiple indices and to present these in multiple ways. It is thus possible to examine children who have low scores on some domains but not all, and those with relative strengths in one domain and weaknesses in another, and so on. Thus the Overall Outcome Index gives an overall summary, while the domain indices account for the fact that development may not be uniform across domains. Further, the continuous and categorical forms of the indices allow flexibility in analytic use.
The illustrative analyses suggest that the Outcome Indices are working as would be predicted, and are capable of discriminating between children living in different circumstances. The versatility of the indices is demonstrated in these examples.
Some limitations in the Outcome Indices should be noted:
- Ability to discriminate between outcomes is stronger at the problem end than the positive end - Many variables in LSAC are designed to identify problematic or below-average child functioning, and their capacity to identify those with particular strengths or above-average functioning is often weak. Hence the final distribution has greater negative discrimination than positive. Further, it was not possible to derive a meaningful index of positive physical outcomes for infants (B cohort) in Wave 1. Care is needed in the interpretation of the positive indices.
- Gaps in infancy data - There are some areas where it was not possible or meaningful to collect outcome information on the B cohort in Wave 1.
- Cut-offs are arbitrary - The categorical form of the Outcome Indices uses cut-offs to identify the top and bottom 15% of the distribution. There is no claim that these proportions are clinically meaningful. They are statistically based, in accord with the common view that one standard deviation below the mean of a population represents significant difficulty. It is therefore not possible to make general claims about the sample overall, such as "X% of children have low social competence" or "Y% of children are in excellent physical health" since the proportions in all cases are pre-defined. However, statements about subpopulations relative to each other are possible.
- The relationship between domains and subdomains is arbitrary - Likewise an assumption has been made that each sub-domain should be equally weighted within each domain and each domain should be equally weighted within the Overall Outcome Index. This does not mean that children will have the same level of problems (or strengths) for each domain, or that each will be equally important for a child's later functioning in life.
- Summary measures reduce complexity - Summary measures such as the LSAC Outcome Indices are convenient, but can oversimplify analyses, causing interesting findings to be missed. Analysts are encouraged to understand what generates the differences observed on the Outcome Indices at the component level before deciding to present findings based on the summary measure.
References
- Australian Institute of Health and Welfare. (2005). A picture of Australia's children (AIHW Cat. No. PHE 58). Canberra: AIHW.
- Cole, T. J., Bellizzi, M. C., Flegal, K. M., & Dietz, W. H. (2000). Establishing a standard definition for child overweight and obesity worldwide: International survey. British Medical Journal, 320, 1240-1243.
- Cole, T. J., Flegal, K. M, Nicholls, D., & Jackson, A. A. (2007). Body mass index cut offs to determine thinness in children and adolescents: International survey. British Medical Journal, 335(7612), 1-8.
- Love, J. (1999). A framework for assessing school readiness outcomes in the context of a National Head Start Impact Evaluation. Washington, DC: Office of Head Start, Administration for Children and Families, US Department of Health and Human Services.
- McCathren, R. B., Warren, S., & Yoder, P. J. (1996). Prelinguistic predictors of later language development. In K. Cole, P. Dale, & D. Thal (Eds.), Assessment of communication and language (Vol. 6, pp. 57-76). Baltimore, MD: Paul H. Brookes.
- Sanson, A., Misson, S., & the Outcome Index Working Group. (2005). Summarising children's well-being: The LSAC Outcome Index (LSAC Technical Paper No. 2). Melbourne: Australian Institute of Family Studies
- Willms, J. D. (Ed.). (2002). Vulnerable children. Alberta: University of Alberta Press.
Lists of tables and figures
List of tables
- Table 1. Measures included in the Outcome Index in each cohort at Waves 1, 2 and 3
- Table 2. Response rates and Cronbach alphas for Health/Physical domain measures
- Table 3. Response rates and Cronbach alphas for Social/Emotional domain measures
- Table 4. Response rates and Cronbach alphas for Learning/Academic domain measures
- Table 5. Correlations of Outcome Indices, intra-wave and cross-cohort
- Table 6. Inter-wave correlations of the Outcome Indices
List of figures
- Figure 1. Conceptual framework for the Outcome Index, showing domains and subdomains
- Figure 2. Percentages identified by the positive and negative Learning/Academic domain cut-offs, by gender, 4-5 year-olds
- Figure 3. Mean scores for the Learning/Academic and Social/Emotional indices, by negative or positive Health/Physical index cut-off, 6-7 year olds
- Figure 4. Change between waves in mean domain indices for K cohort children who lived with both biological parents at Wave 1, by whether parents had separated by Wave 2
- Figure 5. Percentage of children with positive or negative indices, by single- and dual-parent families, 2-3 year olds
- Figure 6. Mean Overall Outcome Index scores, by weekly parental income, 4-5 year olds
- Figure 7. Mean Social/Emotional Outcome Index scores, by Parent 1's rating of their own parenting ability, 0-1 year olds.
- Figure 8. Cohort comparison on cross-cohort Outcome Indices, 4-5 year olds
List of appendix tables
- Table A1. Ongoing conditions used in the Health Problems index, by cohort and child's age
- Table A2. Correlations among Health subdomain standardised scores, including Health Problems index
- Table B1. Numbers of scores with variables missing, for each subdomain with more than one variable for 4-5 year olds (unweighted frequencies)
- Table B2. Means and standard deviations for pre-standardisation subdomain scores, for subdomains that underwent standardisation, by missingness level for 4-5 year olds
- Table B3. Numbers of subdomain scores missing for each domain for 4-5 year olds (unweighted frequencies)
- Table B4. Means and standard deviations for pre-standardisation domain indices, for domains that underwent standardisation by missingness level
- Table C1. Rotated factor solution for BITSEA items
List of appendix figures
Appendix A: Changes from the Wave 1 Indices
Since the publication of the LSAC Technical Paper on the Outcome Indices (Sanson et al., 2005), a number of changes have been made in response to accumulating experience in using the Wave 1 Outcome Index. Those who have read that Technical Paper will have noticed that a change in terminology has occurred. The newly formed Data Expert Reference Group recommended that the focus be taken off the score across all three domains and placed more on the score for each domain. As such, the Health/Physical domain index, Social/Emotional domain index, Learning/Academic domain index and Continuous Outcome Index are now known as the Health/Physical Outcome Index, Social/Emotional Outcome Index, Learning/Academic Outcome Index and Overall Outcome Index respectively. The advent of cross-cohort data for the same age has also meant the distinction between cross-cohort and within-cohort Outcome Indices has become necessary. Additionally, three changes to the calculation of the Outcome Indices have been made:
- a Health Problems index was developed and included in the Health/Physical domain;
- an ordinal Weight Status variable was developed to replace the magnitude of difference from the mean of the Body Mass Index (BMI) used in Wave 1; and
- the number of subdomains in the Learning/Academic domain was simplified from four to two.
This section describes the rationale for these changes.
Treatment of Body Mass Index
When constructing the score for the Wave 1 Health/Physical Outcome Index, it was considered desirable to use a measure that captured both overweight and underweight. The approach taken for the Wave 1 Outcome Index was to convert all the BMI scores to z-scores, take the absolute value of these z-scores and restandardise back to a z-score, with this then reversed so that "good" BMIs had high scores and "poor" BMIs had low scores. The distribution of scores on this measure looked like the left half of a bell curve, with a large number of cases having the highest scores (which consequently weren't very high), and a tail of cases with poor BMIs consisting of both underweight and overweight children.
One consequence of this method of scoring for the BMI is that overweight and underweight children are approximately equally represented in the low scores. However, the Australian Institute of Health and Welfare (2005) reported that among children aged 2-14, 18% of boys and 20% of girls were overweight or obese, while only 7% of boys and 4% of girls were underweight. Another implication is that children with average BMI received slightly higher scores than those who were above or below average. However, provided BMI falls within a "normal" range, there is no evidence that higher or lower weights within the range are harmful.
For this reason, it was decided to create an ordinal variable from the cut-offs developed by Cole et al. for overweight (2000) and underweight (2007). The variable was coded such that children received 1 point if they were Underweight I, 2 points for Underweight II, 3 points for Underweight III, 1.5 points for Overweight, 3 points for Obese, and 0 points for being between the over and underweight cut-offs. In this scoring, children who were underweight received similar scores to those who were overweight. It may be that underweight is less of a problem for a child than overweight; however, quantifying this difference is problematic. It should be noted, however, that more children were classified as overweight.
Index of health conditions
One of the problems encountered in developing the Health/Physical Outcome Index is in the treatment of diagnoses of health problems. From a data analysis perspective, a diagnosis is a binary variable that can mask a range of different health outcomes. For example, one child could have a mild case of asthma that is largely kept in check with medication, while another could have a more serious case that could greatly limit their ability to undertake physical activity, with consequent social and health costs. The first child is unlikely to suffer any long-term damage from their condition, while for the latter the effect on their eventual participation in society could be marked.
In Wave 1, the Health/Physical Outcome Index dealt with this problem by using only general health questions, such as the Overall Rating of Health, and the Special Health Care Needs screener. The Special Health Care Needs screener is particularly problematic since, even though a certain severity of condition is required to qualify for a yes answer, it still produces a binary result. Combining a binary result with continuous scores as done in the Outcome Index means that frequency is mistaken for severity. The fact that a complete absence of problems was most common also means that the variable did not have a normal distribution.
One solution to this problem is to combine a number of diagnoses into a Health Problems index thus creating a continuous measure. The downside of such a measure is that a child with two mild problems might score higher than one with a single very debilitating problem, so breadth of problems and severity are somewhat confounded.
Table A1 contains a list of the conditions used in the Health Problems index. The index is a sum variable with one point given for an asthma diagnosis, one point for diagnosis for each other ongoing condition, and a point for each night spent in hospital (up to 4) not due to an injury (see Figure A1).
| Condition | B cohort | Cross-cohort | K cohort | ||||
|---|---|---|---|---|---|---|---|
| 0-1 years | 2-3 years | 4-5 years | 4-5 years | 4-5 years | 6-7 years | 8-9 years | |
| Hearing problems | X | X | X | X | X | ||
| Vision problems | X | X | X | X | X | ||
| Developmental delay | X | ||||||
| Eczema | X | X | X | X | X | X | X |
| Diarrhoea/collitis | X | X | X | X | X | X | |
| Anaemia | X | ||||||
| Ear infections | X | X | X | X | X | X | |
| Other infections | X | X | X | X | X | X | X |
| Food or digestive allergies | X | X | |||||
| Food or other allergies | X | X | X | X | |||
| Other illnesses | X | X | X | X | X | ||
| Other physical disabilities | X | X | |||||
| Frequent headaches | X | X | X | X | X | ||
| Recurrent abdominal pain | X | X | X | X | |||
| Constipation | X | X | |||||
| Soiling | X | X | |||||
| Tonsillitis | X | X | |||||
Figure A1. Distribution of Health Problems index, by cohort and child's age

Table A2 gives the correlation among the Health subdomain scores, with the Health Problems index included for both Wave 1 and 2. The index correlates well with the other measures, particularly the Special Health Care Needs screener, and is comparable to the other health measures for both waves in its contribution to the Health/Physical domain index.
| Health problems | Overall rating of health | Special health care needs | Weight status | |
|---|---|---|---|---|
| Age 0-1 (B cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.30 | 1.00 | ||
| Special health care needs | 0.39 | 0.21 | 1.00 | |
| Physical Outcome Index | 0.77 | 0.69 | 0.74 | |
| Age 2-3 (B cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.30 | 1.00 | ||
| Special health care needs | 0.46 | 0.26 | 1.00 | |
| Weight status | 0.04 | 0.01 | 0.04 | 1.00 |
| Physical Outcome Index | 0.57 | 0.55 | 0.58 | 0.33 |
| Age 4-5 (B cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.23 | 1.00 | ||
| Special health care needs | 0.41 | 0.25 | 1.00 | |
| Weight status | 0.06 | 0.02 | 0.05 | 1.00 |
| Physical Outcome Index | 0.54 | 0.53 | 0.56 | 0.34 |
| Age 4-5 (cross-cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.27 | 1.00 | ||
| Special health care needs | 0.45 | 0.24 | 1.00 | |
| Weight status | 0.07 | 0.02 | 0.05 | 1.00 |
| Physical Outcome Index | 0.57 | 0.53 | 0.56 | 0.35 |
| Age 4-5 (K cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.26 | 1.00 | ||
| Special health care needs | 0.43 | 0.26 | 1.00 | |
| Weight status | 0.05 | 0.02 | 0.05 | 1.00 |
| Physical Outcome Index | 0.56 | 0.54 | 0.57 | 0.33 |
| Age 6-7 (K cohort ) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.28 | 1.00 | ||
| Special health care needs | 0.43 | 0.25 | 1.00 | |
| Weight status | 0.05 | 0.05 | 0.01 | 1.00 |
| Physical Outcome Index | 0.51 | 0.56 | 0.55 | 0.37 |
| Age 8-9 (K cohort) | ||||
| Health problems | 1.00 | |||
| Overall rating of health | 0.27 | 1.00 | ||
| Special health care needs | 0.42 | 0.23 | 1.00 | |
| Weight status | 0.02 | 0.11 | 0.00 | 1.00 |
| Physical Outcome Index | 0.54 | 0.57 | 0.53 | 0.42 |
Subdomain structure for the Learning/Academic domain
At the time of the development of the Wave 1 Outcome Indices, the domain and subdomain structure was developed with the intention that (at least from age 4-5 years onwards) it would remain consistent throughout future waves. For the Learning/Academic domain, 4 subdomains were chosen: Language, Literacy, Numeracy and Approach to Learning. However, in considering the classification of some Wave 2 outcome measures, this structure came up against three problems:
- Does the Academic Rating Scale of Language and Literacy belong in the Language or the Literacy subdomain?
- In which subdomain does the Matrix Reasoning test belong?
- Does the WAI measure Approach to Learning, and is Approach to Learning an appropriate subdomain?
The solution to the first problem was to merge two of the subdomains into a single Language and Literacy subdomain. Given the close relationship between the two concepts, this is justifiable on theoretical grounds, and provides the Learning/Academic domain with a more even balance between maths and science on the one hand and language and literacy on the other. The second problem was dealt with by expanding the numeracy subdomain to become Numeracy and Cognition.
This organisation of the subdomains within the Learning/Academic domain as Language and Literacy and Numeracy and Cognition, was adapted from a framework for assessing school readiness in the Head Start Impact Evaluation Study in the United States (Love, 1999). While this framework does not explicitly use these titles for its domains, it does identify literacy as a performance area in relation to language development and numeracy as a performance area in relation to cognitive development.
In Wave 1, the WAI was classified as a measure of Approach to Learning, since it tapped school-related learning largely acquired in non-school settings, such as home and child care/preschool rather than a formal school situation, and required the child to be able to undertake a school-like assessment (with appropriate concentration and effort). However, further consultations suggested that it is better classified as a test of Language and Literacy since most of the tasks involved fall into these fields. Moving the WAI out of Approach To Learning meant removing the Approach To Learning subdomain entirely for the children before they arrive at ages 6 to 7.
Approaches to Learning is conventionally thought of as predispositions and learning styles that influence the way the child thinks and acts upon learning opportunities. It encompasses predispositions (e.g., temperament) and learning styles (e.g., task persistence), both of which are already covered in the Social/Emotional domain.
Changing the subdomain structure between waves is not ideal, given that the purpose of the domain structure is to provide consistency of meaning in the Outcome Indices from wave to wave. However, it is anticipated that this new subdomain structure for learning will be able to be consistent through the upcoming waves (as will be those in the Health/Physical domain and the Social/Emotional domain).
Appendix B: Handling missing data
This appendix describes the procedures adopted to ensure that the presence of missing data did not skew results. The calculation of the 4-5 year old within-cohort Outcome Indices for the K cohort is used here as an example.
In cases where one or more z-scores in a subdomain were missing, a subdomain score was still obtained by taking the average of all the available z-scores. However, when averaging, the standard deviation of the mean score increases as the number of scores averaged decreases. Hence, children with more missing data for a subdomain would tend to have scores further from the average value, without this being a reflection of their actual outcomes. To correct for this, a variable was calculated for each subdomain with more than one variable, indicating the number of variables missing for each case. The frequencies of these variables can be seen in Table B1. These variables were used as grouping variables to divide the file by level of "missingness" for each subdomain. A standard deviation score was then obtained for each level of missingness, which was used to divide the subdomain score. This method of standardisation corrects for the greater standard deviation obtained when averaging fewer z-scores, without disguising any mean differences present in the data.
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| Health | 4,876 | 103 | 1 | 2 |
| Social Competence | 4,969 | 0 | ||
| Externalising | 4,969 | 0 | ||
| Language and Literacy | 4,376 | 527 |
Note: For ease of interpretation, frequencies indicating that scores for all component variables of the subdomain are missing are excluded from the above table.
It can be seen from Table B1 that there is no partially missing data for the Externalising and Social Competence subdomains, but large amounts for Language and Literacy, and a moderate amount for Health. Due to insufficient numbers to reliably standardise scores, those with 2 and 3 missing variables on Health were merged with those with 1. Mean and standard deviation scores for each subdomain and level of missingness are presented in Table B2. Note that post-standardisation, the standard deviation for each subdomain and each missingness level is 1, while the mean equals the pre-standardisation mean divided by the pre-standardisation standard deviation. For example, post-standardisation, the mean for the Health subdomain score for those with no missing data is .01⁄.61 = .02 and the standard deviation is 1. At this stage, each subdomain score was restandardised to have a mean of 0 and a standard deviation of 1 (i.e., a z-score) to correct for minor fluctuations from these values due to taking averages and the standardisation process.
| 0 | 1 | |||
|---|---|---|---|---|
| Mean | SD | Mean | SD | |
| Health | .01 | .61 | -.39 | .91 |
| Language and Literacy | .02 | .78 | -.35 | 1.18 |
The above approach is repeated to standardise by missingness level when combining subdomain scores into domain indices. The frequencies for the missingness variables for each domain can be seen in Table B3.
| 0 | 1 | 2 | |
|---|---|---|---|
| Health/Physical | 4,198 | 784 | |
| Social/Emotional | 4,968 | 1 | 0 |
| Learning/Academic | 3,147 | 1,785 |
Note: For ease of interpretation, frequencies indicating that all subdomain scores of the domain are missing are excluded from the above table.
Only one case was missing a subdomain score for the Social/Emotional domain where other subdomain scores were present; however, a number of cases with some data were missing subdomain scores in the Health/Physical and Learning/Academic domains. The means and standard deviations for the different levels of missingness for the Health/Physical and Social/Emotional domains can be seen in Table B4. Scores at each missingness level were divided by their standard deviation.
| 0 | 1 | |||
|---|---|---|---|---|
| Mean | SD | Mean | SD | |
| Physical | .01 | .77 | -.07 | 1.05 |
| Learning | .05 | .82 | -.16 | 1.07 |
Figure B1 shows the proportion of children identified by each of the cut-offs based on the amount of missing data for the Outcome Indices with the above corrections versus what would have been the case if these corrections hadn't been performed. The most important thing to note is that cases with no or very little missing data are more likely to be identified by the cut-offs when the correction has occurred, while those with more missing data are less likely to be identified. Secondly, for the Learning/Academic Outcome Index and Overall Outcome Index cut-offs, those with more missing data are more likely to be identified by the negative cut-offs and less likely to be identified by the positive cut-offs. This reflects the tendency for cases with more missing data to score more poorly on the variables they do have present. For the Health/Physical Outcome Index, cases with missing data were more likely to be identified by both cut-offs. This was due to 30% of cases scoring full marks for the Health subdomain. This lack of discrimination meant that there was a group of these cases that didn't have a Motor subdomain score that were included as being above the cut-off, even though it would be expected that some may have fallen below the cut-off if they had had this data. It should be noted, however, that this trend would have been more pronounced if the correction had not occurred.
Figure B1. Percentage of children identified by positive (+) and negative (-) cut-offs, by number of original variables missing for 4-5 year olds, for Health/Physical, Learning/Academic and Overall Outcome Index cut-offs
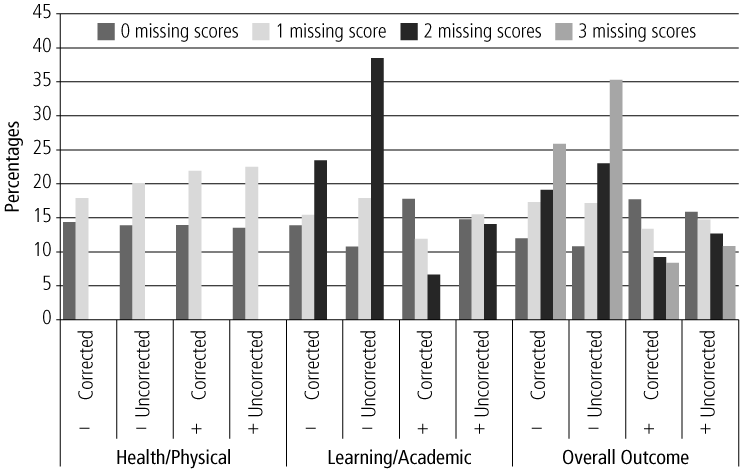
Note: The Social/Emotional domain did not have enough missing data to be meaningfully included. Due to low numbers, cases with more than 1 missing data were included with the 1 missing group)
Appendix C: BITSEA factor analysis
In order to determine whether the BITSEA could be broken down into subdomains, and to determine which items corresponded to which subdomain, a maximum likelihood factor analysis using varimax rotation was performed with Statistical Analysis Software (SAS). Table C1 shows the rotated factor solution for this analysis. The first of these contains items tapping whether the child exhibits various non-compliant, overactive or aggressive behaviours and therefore is labelled "Externalising". The second assesses the extent to which the child is frequently unhappy, fearful and anxious, and so is labelled "Internalising". The third factor is basically all the items from the BITSEA Competence subscale, tapping adaptable, prosocial behaviour and social communication, and so is labelled "Social Competence". Items loading on to a factor of .30 or higher, or -.30 or lower, were included in the new derived subscales.
| Factor 1 (Externalising) | Factor 2 (Internalising) | Factor 3 (Social Competence) | |
|---|---|---|---|
| Shows pleasure when he/she succeeds (e.g., claps for self) | -0.03 | -0.11 | 0.39 |
| Gets hurt so often that you can't take your eyes off him/her | 0.29 | 0.17 | -0.08 |
| Seems nervous, tense or fearful | 0.00 | 0.48 | -0.03 |
| Is restless and can't sit still | 0.40 | 0.12 | -0.12 |
| Follows rules | -0.34 | -0.02 | 0.33 |
| Wakes up at night and needs help to fall asleep again | 0.21 | 0.23 | 0.11 |
| Cries or tantrums until he/she is exhausted | 0.34 | 0.28 | -0.04 |
| Is afraid of certain places, animals or things | 0.02 | 0.46 | 0.02 |
| Has less fun than other children | 0.03 | 0.29 | -0.14 |
| Looks for you (or other parent) when upset | 0.05 | 0.14 | 0.20 |
| Cries or hangs on to you when you try to leave | 0.21 | 0.36 | -0.04 |
| Worries a lot or is very serious | 0.03 | 0.51 | -0.04 |
| Looks right at you when you say his/her name | -0.10 | -0.02 | 0.36 |
| Does not react when hurt | 0.09 | 0.07 | -0.15 |
| Is affectionate with loved ones | -0.07 | -0.12 | 0.35 |
| Won't touch some objects because of how they feel | 0.01 | 0.30 | -0.04 |
| Has trouble falling asleep or staying asleep | 0.27 | 0.26 | 0.07 |
| Runs away in public places | 0.44 | 0.00 | -0.12 |
| Plays well with other children (not including brother/sister) | -0.10 | -0.18 | 0.35 |
| Can pay attention for a long time (not including TV) | -0.24 | 0.01 | 0.33 |
| Has trouble adjusting to changes | 0.12 | 0.43 | -0.10 |
| Tries to help when someone is hurt (e.g., gives a toy) | -0.03 | 0.00 | 0.42 |
| Often gets very upset | 0.27 | 0.40 | -0.06 |
| Gags or chokes on food | 0.10 | 0.19 | -0.09 |
| Imitates playful sounds when you ask him/her to | -0.01 | -0.09 | 0.50 |
| Refuses to eat | 0.25 | 0.24 | -0.05 |
| Hits, shoves, kicks or bites children (not including brother/sister) | 0.42 | 0.07 | -0.10 |
| Is destructive; breaks or ruins things on purpose | 0.49 | 0.09 | -0.07 |
| Points to show you something far away | 0.03 | -0.03 | 0.43 |
| Hits, bites or kicks you (or other parent) | 0.60 | 0.09 | -0.04 |
| Hugs or feeds dolls or stuffed animals | -0.08 | -0.01 | 0.41 |
| Seems very unhappy, sad, depressed or withdrawn | 0.11 | 0.31 | -0.11 |
| Purposely tries to hurt you (or other parent) | 0.51 | 0.08 | -0.03 |
| When upset, gets very still, freezes or doesn't move | 0.08 | 0.25 | -0.01 |
Note: Factor loadings ≥ .30 have been highlighted to assist in the readability of the table.
Sebastian Misson, at the time of writing, was the Data Manager for LSAC at the Australian Institute of Family Studies.
Professor Ann Sanson is at the Department of Paediatrics, University of Melbourne. Ann was at the Australian Institute of Family Studies from 2000 to 2004, holding the roles of Principal Research Fellow, Deputy Director and Acting Director. As LSAC Project Director, she also led the early development work on LSAC. She now fills the role of LSAC Principal Scientific Adviser, and leads the LSAC Child Functioning Design Team.
Associate Professor Donna Berthelsen is a researcher in the Centre for Learning Innovation and a lecturer in the School of Early Childhood at Queensland University of Technology. She is the leader of the LSAC Education Design Team.
Associate Professor Melissa Wake is Director of the Research and Public Health Unit at the Centre for Community Child Health, Murdoch Childrens Research Institute, and leader of the LSAC Health Design Team.
Dr Helen Rogers is a Principal Researcher/Section Manager in the Research and Analysis Brach of the Department of Families, Housing, Community Services and Indigenous Affairs.
Dr Sheldon Rothman is a Principal Research Fellow at the Australian Council for Educational Research, where he manages the Longitudinal Surveys of Australian Youth project.
Mark Sipthorp is the Data Manager for LSAC at the Australian Institute of Family Studies.
LSAC Research Consortium
The LSAC Research Consortium comprises: Dr John Ainley, Professor Michael Bittman, Dr Bruce Bradbury, Dr Linda Harrison, Associate Professor Jan Nicholson, Dr Bryan Rodgers, Professor Michael Sawyer, Associate Professor Ann Sanson, Professor Sven Silburn, Dr Lyndall Strazdins, Associate Professor Judy Ungerer, Professor Graham Vimpani and Professor Steve Zubrick.
Misson, S., Sanson, A., Berthelsen, D., Rogers, H., Rothman, S., Sipthorp, M., Wake, M., & the LSAC Research Consortium. (2011). Tracking children's development over time: The Longitudinal Study of Australian Children Outcome Indices, Waves 2 and 3 (Research Paper No. 50). Melbourne: Australian Institute of Family Studies.
978-1-921414-66-4